Source (restricted to non-HBO-Max regions)
Kamala Harris is known to love Venn diagrams and would be cringing hard at this.
For reference, circles in Venn (Euler) diagrams are sets of objects with a certain property. Select objects are shown inside or outside of each circle depending on whether they belong to the set.
A good example is xkcd 2962:
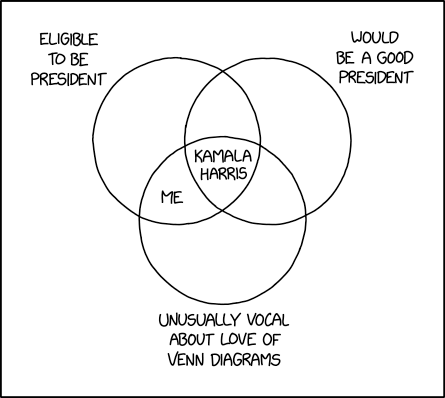


I’m not saying either is good use of Venn diagrams (as opposed to the provided xkcd comic). A better “mathematical” way to express the relation is simply “KAMA + BLA = KAMABLA” (yes, the mathematical sign “+” is not used for concatenation in math but you get the point).
The tweet would work if we assume:
Is it a technically correct Venn diagram? I’d say it could be, given the above weird assumptions.
Is a Venn diagram the correct tool for the job? No.
As for JO’s example with sea creatures: if we assume
JO’s example might work if
However, this essentially turns around the convention “sets are defined by properties and include objects” to “sets are defined by objects and include their properties”, which is in my opinion even more cringey than considering “words containing ‘BLA’” a notable set. (From a mathematical standpoint. The entire “Kamabla” thing is pure cringe in the practical sense.)
I think this is a good explanation of why JO is wrong, which I was not expecting.
This was my exact thought as I was watching but totally let it pass when he gave his “solution” without another thought before now.
However I still don’t think the tweet works. Your logic is sound but the diagram would need to label sets A and B with “Words that include…”
Of course that would just further expose it as unfunny and pointless.
ETA: I notice you edited the comment while I was replying. Hoping you didn’t change the substance too much - I don’t have time at the moment to figure out what changed and see if my response still applies 😅🤞